| Easy : for the curious |
The group structure is a fundamental concept, used widely and outside mathematics. It is very often used in physics, and we shall see an example of an important group of the theory of special relativity, in a forthcoming article .
Meanwhile, we will simply give the definition and a few simple examples.
What is a group ?
An example of very important mathematical object is that of a group. A group is a set with a precise structure. There is two ways to define in a general sense what we call a structure :
$\bullet$ the first consists in defining operations on the sets, linking the elements of the set or linking subsets. That is a way to define a particular geometry. One defines relations between the elements called "points" and subsets called "straight lines" : belonging, intersection, etc. Then we postulate precise properties of these operations in order to form a coherent logical system : two straight lines intersect by at least one point, any straight line contains at least three points, etc. We are then building a geometrical structure.
$\bullet$ the second way consists in defining one or more composition laws on the elements of the set. A composition law is a n-ary operation that takes any given number of elements of the set and combines them to form a single element. The properties of these operations give rise to a particular structure, called an abstract structure.
A group is an abstract structure on a set $G$, whose operation $\circ $ satisfies :
- it is a binary operation, that is to say it takes two elements of the set to make a third. If we name those elements $a$ and $b$, then we have $a\circ b$ as the result of the binary operation.
- it is closed, so for any given $a,b\in G$ then $a\circ b\in G$.
- it verifies the property of associativity, that is to say for any given $a,b,c\in G$, then $(a\circ b)\circ c=a\circ (b\circ c)$.
- there exists an identity element $e$ so that for each $a\in G$, $a\circ e=e\circ a=a$.
- for each $a\in G$, there exists an element $d\in G$ so that $a\circ d=d\circ a=e$. It is the inverse element of $a$ for the operation $\circ $.
For example, the set of all integers $\mathbb Z$ forms a group for the operation of addition $+.$ Its identity element is $0$ and inverse elements are negative numbers. However, it is not a group for the operation of multiplication $\times$.
The set of all rational numbers $\mathbb Q$ is a group for multiplication. The identity element is $1$ and the inverse element of a rational number $q=\frac xy$ is the inverse quotient $q^{-1}=\frac yx$. What's more, $\mathbb Q$ is also a group for the operation $+$.
There exists groups of a finite number of elements, which are easier to study but nonetheless very interesting.
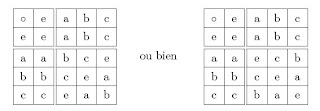
For example, there is only two groups of four elements. They are entirely characterized by their Cayley table, given by (with $e$ the identity element and $a,b,c$ the three other elements) :
The first table defines a group of order four called "cyclic" because each element can be written as the iteration of a generating element, and the group is noted
$$\mathbb Z_4\simeq\{a, a^2, a^3, a^4=e\}.$$
The second one is called Klein's group and designed by
$$\mathbb D_2\simeq\mathbb Z_2\times \mathbb Z_2\simeq\{a, b, a\circ b, a^2=b^2=e\}.$$
This abstract structure, combining a well defined set of operations on all elements can be interpreted geometrically.The two types of structure we mentioned earlier are strongly linked. We will come back in detail to this general relation between geometrical and abstract structure with a future article about what mathematicians call the Erlangen Program.
Meanwhile, we will only see a short example of this relation.
Geometrical interpretation of Klein's group
Let's consider some geometrical transformations, or symmetries in the plane. Let's call $e$ the trivial symmetry that doesn't change a thing, the identity element; $a$ and $b$ two reflection symmetry of perpendicular axis; and $c$ a rotation of angle $180^\circ$ around the intersection point of the two precedent axis.
If we consider the operation $\circ $ as the law of composition of two geometrical transformations, then they form a group, and more precisely a Klein group. Indeed, the reflection symmetries and the two-fold rotational symmetry are involutary, that is to say $a\circ a=e$, $b\circ b=e$ and $c\circ c=e$. Note that we of course have $a\circ b=c$.
In other terms, the set of all symmetries of a (non square) rectangle, which are also its isometries in the plane, form a Klein group of order $4$. :
A lot of objects have these symmetries. Note that we not only speak of spatial symmetries, but also of permutation symetries.
The mattress group
A mattress possesses such symmetries. In three dimensional space this time we consider three rotations $a,b$ and $c$ of perpendicular axis. We even use these transformations of the Klein group : to sleep with the most comfort and assure a long life span to your mattress, you need to rotate it regularly to flatten out the dents and fill in the troughs. And it's not enough to rotate it only one time. One also needs to change its orientation so that the weight doesn't act at the same place each time.
But the thing is that it only needs to be done one or two times a year, so we never remember how we rotated it last...
Some people recommend to do a rotation $c$ each spring and a reflection $a$ or $b$ each autumn, a system which works pretty well, but some recommend some pretty complicated and often uneffective method... So what to do ?
The answer is remarkably simple : just label the corners ! It only takes to mark each corner of each face of the mattress by the numbers from $1$ to $4$ and then to count from $1$ to $4$ at a fixed corner with the appropriate movements !
The mechanic's group
Let's number all four wheels of a car from $1$ to $4$ this way :
If we write $(12)$ the permutation of wheel $1$ with wheel $2$, we can do the operations $(12), (34), (12)(34), (13)(24), (14)(23)$.
However, the two wheels of an axle must stay on an axle and not be separated, because the car's geometry, wheels alignment and one's driving may cause each tire to wear differently, and the traffic laws in France require that the tires of a common axle do not present a big difference in wear, so people are advised to watch over a uniform wearing of tires.
So the permutations $(13), (14), (23), (24), (1234), (1243), (1324), (1342)$, $(1423), (1432)$ are not possible. The last six being cyclic rotations of the four wheels. The cyclic rotations of three wheels $(123), (124), (132), (134), (214), (234)$, $(243), (314)$ are also not possible.
The permutations $a=(13)(24), b=(12)(34), c=(14)(23)$ and the identity element form a Klein group. With the additional permutation $d=(12)$, the group extends with $(34)=(12)(34)\circ (12)$, $(1432)=(13)(24)\circ (12)$ and $(1324)=(12)\circ (13)(24)$.
So the group of all the authorized permutations of wheels, which we will call the mechanic's group is
$$\mathbb D_4\simeq\mathbb Z_4\rtimes \mathbb Z_2\simeq\{a,b,a\circ b,d,b\circ d,a\circ d,d\circ a,e\}.$$
Of course, a designer of mattress or a mechanic doesn't need symmetry groups in their every day work ! However, they are useful as soon as we want to understand the profound logical and geometrical relations between objets and the space in which we conceive them. We will see in a next article a more profound and complex use of abstract groups in physics, with the example of the transformations of the theory of relativity.





Post a Comment
You can use HTML tags b, i, a.