The group of special relativity

Medium : for amateurs

In its modern interpretation, the principle of relativity is profoundly linked to the group structure of Lorentz transformations.

We will describe the equivalence relation between the two, and at the same time give a geometrical description of what is an inertial reference frame in special relativity.

The principle of relativity

$\bullet$ Original formulation : « the same laws of electrodynamics and optics will be valid for all frames of reference for which the equations of mechanics hold good. »
(A.Einstein, On the electrodynamics of moving bodies, 1905)


« The laws by which the states of physical systems alter are independent of the alternative, to which of two systems of coordinates, in uniform motion of parallel translation relatively to each other, these alterations of state are referred »
(A.Einstein, Does the inertia of a body depend upon its energy-content ?, 1905)

This formulation implies a precise mathematical relation between the inertial frames of reference, which is given by the Lorentz transformations ¹.
However, it was not clear at the time that it also implied, with a profound meaning, a group structure of these transformations, except for some brilliant mathematicians like Henri Poincaré ² (1854-1912), Hermann Minkowski (1864-1909) or Félix Klein (1849-1925). It became central only with late modern works.


$\bullet$ Modern formulation : « There exists an infinite continuous class of reference frames in space-time which are physically equivalent. »
(J.M.Levy-Leblond, One more derivation of the Lorentz transformation, 1975)



Now two words give an important clue as to the meaning of this formulation : "class" and "equivalent". Let's use a little bit of formalism : if the set of all reference frames is called $X$, and the equivalence relation $\doteq$, then :

Two reference frames $F,F^\prime\in X$ are said equivalent, noted $F\doteq F^\prime$ if and only if all the laws that refer to it are of identical form (identified with a same mathematical function of the physical quantities).

It's important to see that each couple of reference frame can be associated with a general transformation of the physical quantities from the first to the second reference frame (a change of reference frame).

The principle of relativity states that if we take any two inertial reference frame, the corresponding transformation (called inertial) will keep the form of the function that defines any particular given law. It also means that the properties of the equivalence relation $\doteq$ will determine the properties of the general transformations.

Namely, the principle of relativity (in its modern, more general form) causes the set of general transformations from a reference frame to another to form a group (it is even equivalent to that fact) : the reflexivity of the relation ($\forall F\in X, F\doteq F$) shows the existence of an identical general transformation, its transitivity

$\forall F,G,H\in X \text{, if }F\doteq G\text{ and }G\doteq H\text{, then }F\doteq H$

shows the associativity of the general transformations, and eventually its symmetry

$\forall F,G\in X\text{, if }F\doteq G\text{, then }G\doteq F$

shows the existence of inverse general transformations.

A specific type, or class of reference frames, say, inertial reference frames, will then imply a specific type of transformations. In this case, these transformations are, as you guessed, the Lorentz transformations (inertial changes of reference frame).

What is an inertial reference frame ?

A reference frame can be abstracted as a coordinate system. So in the set of all physical events, depicted by a four dimensional space-time, it is given by five affinely independent points ³. One will be called the origin, and the four others will define the unity of each axis. Then we only need four numbers each time we need to refer in a univocal way to a single event.

For reasons of simplicity and to best match reality through the topological properties of space-time, we use real numbers. If we assume that the laws of physics are the same in each position in space-time without exceptions, it means mathematically that the group of general transformations acts "transitively" on the set of all events (space-time). Without further mathematical description of this "transitive action", let's just say that we need a homogeneous space-time, or mathematically speaking, an affine space.

An affine frame in the four dimensional affine space is simply given by five affinely independent points ³, and depicts a reference frame. So the set of all physical reference frames is depicted by the set of all affine frames.

Edit : Let's look at an affine frame from a geometrical point of view. In one dimension, it's just two distinct points. The origin of the frame is not fixed and can be any of the two points. In two dimensions, an affine frame is three non aligned points, and any one of them could be the origin. One-dimensional affine frame Two-dimensional affine frame These frames are not oriented. To orient a one dimensional affine frame simply consists in choosing a point for the origin, so there is only two possibilities : One-dimensional oriented affine frames To orient a frame in greater dimension one needs not only to choose a point of origin, but also to orient its axis. For example here are two of many possibilities in two dimensions : Two two-dimensional oriented affine frames

Now let's take a particular oriented affine frame and use it as an orientation reference to define by convention the orientation of the first three axis of all other frames, which will now be called space-oriented (affine) reference frame. It's equivalent to choose an orientation of space for all of our affine frames, or geometrically to choose a reference direction (clockwise or anti-clockwise) for any rotating movement in space. Basically we are saying that no change of reference frame should invert the chirality of a phenomenon (we are only speaking of macroscopic phenomenon, not dealing here with quantum mechanics which has different needs).

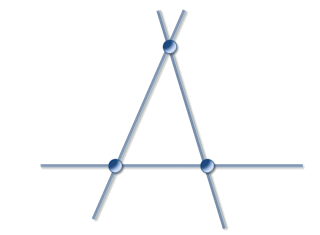
Edit : We then have partially oriented frames. For example, in two dimensions such a frame could be : A two-dimensional semi-oriented affine frame

Finally, let's take a particular space-oriented four-dimensional affine frame and use it as a reference to define the orientation of the last (fourth) axis or all other frames, which will now be called space-time-oriented (affine) reference frames. It's equivalent to choose an orientation of time for our (already space-oriented) affine frames, or geometrically to choose a reference direction for any movement in time. Basically we are saying that no change of reference frame should reverse time, or invert the entropy of a phenomenon (again, we are only concerned with macroscopic phenomenon here).

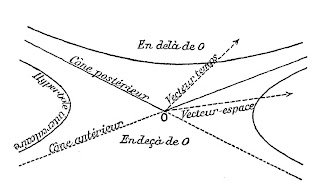
To take account of the causal structure of physical events, one needs to add to this affine space-time a metric structure. The way to fix its metric is to determine the particular metrical relations between the coordinates of any point in an affine frame. It can be done by stating that the distance between two points

$X=(x, y, z, t)$ and $X^\prime=(x^\prime, y^\prime, z^\prime, t^\prime)$

is

$d(X,X^\prime)^2=(x-x^\prime)^2+(y-y^\prime)^2+(z-z^\prime)^2-(t-t^\prime)^2$.

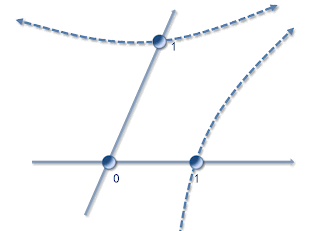
Edit : It is also equivalent to state that the unit distance from the origin is taken on a unit hyperboloid. In two dimensions, here is what it would look like (each point on a branch of hyperbola is at unit distance from the origin) : Two-dimensional oriented affine frame with a metric

So we just defined mathematically what is an "inertial reference frame" : it is a space-oriented, time-oriented, affine reference frame so that their time and space components are linked by a metric relation required by the causal structure of events. The Lorentz transformations thus are the affine transformations that preserve space orientation and time orientation, and also preserve the causal structure of space-time (that is the metric relations between space and time dimensions of space-time).

The Lorentz group

Now that we know exactly what is mathematically speaking an inertial reference frame, we should easily be able to determine the group of all Lorentz transformations. It is going to be a subgroup of the affine group, containing all of the affine transformations of a real four dimensional affine space, group that we note $GA_4(\mathbb R)\simeq \mathbb R^4\ltimes GL_4(\mathbb R)$. It contains the space-time translations and all of the invertible linear transformations (so the four by four invertible matrices).
The skewed multiplication symbolises the fact that there can be problems of commutation between translations and linear transformations. Important though it is, we will not describe this particularity any further.

Since we need our transformations to respect the causal structure, or the geometry of space-time, these need to leave unchanged the quadratic form $x^2+y^2+z^2-t^2$, and this restriction gives us another subgroup we note $\mathbb R^4\ltimes O(3,1)$. It is called the full Poincaré group (the proper Poincaré group is the one without translations).

Then to keep the space-orientation of our reference frames, the matrices need be of unit determinant (they are called the proper linear transformations), so we have the subgroup noted $\mathbb R^4\ltimes SO(3,1)$. Then again, and finally, to preserve our time-orientation we restrict to the subgroup $\mathbb R^4\ltimes SO_o(3,1)$ called the full Lorentz group. The lower indice $0$ is here to point out that it is the connected component of the identity in the full Poincaré group. It contains, alongside the translations, the proper and orthochronos linear transformations.



So it is this particular group that acts (in a mathematical sense) on the space-time of relativistic physics. It defines and identifies with the geometrical structure of space-time. We will see in a future article about the Erlangen program, the profound link between the concept of group and the geometry of any mathematical space, encompassing that particular one of special relativity.
Of course it also poses interesting questions about its generalization : why a different group for quantum special relativity ? is there a group at the center of general relativity ? We then can see how much the abstract mathematical objects are fondamental to our comprehension of the laws of physics.

Notes :

1. Lorentz transformations are usually described in the particular case of reference frames which have a same origin, parallel axis and the movement being restricted to only one spatial axis. These are the special Lorentz transformation or "boosts". If we note $(x,y,z,t)$ the coordinates of a first reference frame and $(\xi,\eta,\zeta, \tau)$ those of the new frame :
$\tau=\dfrac{t-\frac{vx}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}$, $\xi=\dfrac{x-vt}{\sqrt{1-\frac{v^2}{c^2}}}$, $\eta=y$, $\zeta=z$.
When the movement is not restricted to only one axis, with a velocity vector $V=(v_{_x},v_{_y},v_{_z})$ of norm $v$ :
$\tau=\dfrac{t-\frac{V\cdot X}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}$,
$\xi=x+\dfrac{\frac{v_{_x}}{v^2}V\cdot X-v_{_x}t}{\sqrt{1-\frac{v^2}{c^2}}}-\frac{v_{_x}}{v^2}V\cdot X$,
$\eta=y+\dfrac{\frac{v_{_y}}{v^2}V\cdot X-v_{_y}t}{\sqrt{1-\frac{v^2}{c^2}}}-\frac{v_{_y}}{v^2}V\cdot X$,
$\zeta=z+\dfrac{\frac{v_{_z}}{v^2}V\cdot X-{v_{_z}t}}{\sqrt{1-\frac{v^2}{c^2}}}-\frac{v_{_z}}{v^2}V\cdot X$
where $X=(x,y,z)$ and $V\cdot X=xv_{_x}+yv_{_y}+zv_{_z}$.
The general transformations, fit to any reference frame contain also a rotation of the axis, and then trigonometric functions $\cos$ and $\sin$. The formulas are starting to get heavy ! This is an inconvenience that disappears with the abstract matrix representation of the Lorentz group.

2. Note that Henri Poincaré was already looking for all the invariants of the Lorentz group, using infinitesimal generators (which relates to the Lie algebra approach of our days) ! and this in 1905 (see our second bibliographic reference), the same year Einstein published his article, which Poincaré had still no knowledge...
However, let's not make the mistake of attributing relativity theory to Poincaré, since he never built any complete theory (in physics anyway), and was merely correcting and improving other physicists' work (Maxwell, Lorentz, etc.). We will get back to this often neglected matter of the history of physics in a later article, with lots of details and references.

3. $n$ points are said affinely independent if any subset is affinely independant. For exemple, two distinct points are affinely independant. So are three distinct non-aligned points; four distinct non-coplanar points of which no triplet of points are aligned; five non-hypercoplanar points (which do not belong to a same hyperplane) of which no quadruplet of points are coplanar and no triplet of points are aligned; etc.

Bibliography :

• A.Einstein, On the electrodynamics of moving bodies, John Walker's edition, based on the english translation in the book The principle of relativity, Methuen and company, Ltd. of London, 1923. Genuine Deutch publication Zur elektrodynamik bewegter körper, Annalen der Physik, June 20th 1905.

• H.Poincaré, La dynamique de l'électron, Comptes Rendus des Séances de l'Académie des Sciences de Palerme, 1905. Genuine publication in Rendiconti del Circolo Mathematico di Palermo, t.21, p129-175, 1906 (received July the 23th 1905, printed December 14th 1905).

• H.Minkowski, Space and time, Annales scientifiques de l’E.N.S. 3e série, tome 26, 1909, p. 499-517. French translation of A.Hennequin et J.Marty, 1909. Based on the posthumous edition of M.A.Gutzmer, B.-G. Teubner, Leipzig, 1909. Genuine talk given at the 80th reunion of Deutch naturalists and physicians, Cologne, 1908.

• J.M.Levy-Leblond, One more derivation of the Lorentz transformation, American Journal of Physics, vol. 44, num. 3, p271-277, 1975.

• J.P.Lecardonnel, Un autre point de vue pour présenter la transformation de Lorentz, Bulletin de l'union des physiciens, num. 615, p1171-1196, 1979.

• J.Colombano-Rut, La mathématisation de la mécanique relativiste, term paper (not published), 2009.

Edit : the definition of the metric has been corrected.

Tweeter