| Easy : for the curious |  |
 |
There is no satisfying definition of the general concept of number. However, lots of particular numbers can be rigorously defined. Natural numbers, integers, imaginary, transcendent, algebraic, computable numbers, etc. In this "story", we will see examples of numbers and will try to understand them intuitively and visually. This first episode is about natural numbers.
The "natural number" is a concept that fulfills two needs : that of ordering, and that of comparing sets "in power", i.e. by counting.
For the first need, one defines the ordinal numbers, for the second the cardinal numbers. These two notions seem at first hand to be different faces of the same objects...
The ordinal numbers
Now that we have a "general idea" of what is a number, we can rigorously define ordinal numbers, using two concepts : that of set and of powerset (the set of all subsets). The definition is a little bit formal, but has the advantage of showing that a number can be very different from what we expect...
First, let's call "ordinal number 0" the empty set noted $\varnothing$.
The next ordinal number, 1, is the powerset of $\varnothing$, that is to say the set $\{\varnothing\}$ containing only $\varnothing$.
The next ordinal number, 2, is the powerset of $\{\varnothing\}$, that is to say the set $\{\varnothing,\{\varnothing\}\}$. It contains "0" the empty set $\varnothing$ and "1" its powerset $\{\varnothing\}$.
And we continue, the next ordinal, 3, is $\{\varnothing,\{\varnothing\},\{\varnothing,\{\varnothing\}\}\}$.
Etc.
It quickly becomes tiresome, but is a rigorous definition of ordinal numbers. They form an ordered set, allowing us to count in an orderly fashion since each ordinal contains the preceding ones :
 |
| The first six ordinal numbers |
So, regardless of the objects being sets, points or more complex things like apples or marathon runners, all that characterizes the concept of ordinal number is order.
 |
| Which came first ? |
A simple way of seeing the importance of order is to shake a set of Russian dolls... they cannot change their order :
|
An ordinal number is just a well ordered set. An order is a mathematical relation that verifies some specific axioms 2, and "well ordered" means that every non empty subset has a least element in that ordering. From any ordinal, the concept of order permits us to define its successor. This concept is then locally constructed, by consecutive steps.
Locally means "in a neighborhood" or "as near as we want". There is a formal mathematical definition of this concept in topology, but we only need to understand that here we need a reference point in our construction. An ordinal number is defined as the successor of another, and all starts with the zero, but we only need to see the part of the line containing a reference point :
For example the mailman, when he delivers, only needs to know the number of one house to locate the next house in the street.
|
The cardinal numbers
Now, let's get to cardinal numbers. These can be defined with sets and the concept of equipotence, or bijection. There exists a bijection between two sets if there is a one-to-one correspondence between the elements of each, so when they are equinumerous. For example :
 |
| Bijection between two sets of three elements |
We define cardinals by means of the ordinals :
The cardinal number 0 is the number of elements of $\varnothing$ the ordinal 0.
The cardinal number 1 is the number of elements of $\{\varnothing\}$ the ordinal 1.
The cardinal number 2 is the number of elements of $\{\varnothing,\{\varnothing\}\}$ the ordinal 2.
etc.
 |
| The first six cardinal numbers |
Contrary to the ordinals, there is no order involved here. Like if we shake a can of marbles and make a mess, the cardinality doesn't change :
|
We can see that by definition ordinal numbers and cardinal numbers are the same. Nothing really surprising, but it will not be the case for infinite numbers... We'll see that in a future article.
 |
| Ordinal and cardinal numbers are "the same" the = symbolizes here a bijection |
So, whatever the nature of the counted objects, what characterizes the concept of cardinal number is the bijection between the sets, function that links the elements of the sets. By this notion of function, one can construct the concept of cardinal numbers globally.
Arithmetic of ordinal numbers
Let's consider a point on a straight line, representing the ordinal number 0. By defining each next ordinal with a translation on the line, in any fixed direction and of any length that is not zero, one can construct every finite ordinal number. Once the direction is chosen, the length doesn't matter and can vary, as long as it stays finite and not null, hence unchanging the order of the points. Here is such a picture of ordinal numbers :
 |
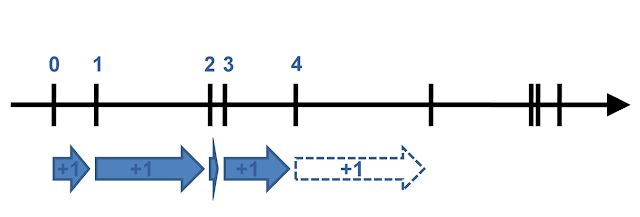| Four translated ordinal numbers |
In this particular geometric picture (we can imagine different ones), to add the ordinal numbers $x$ and $y$ is to slide $y$ times the point $x$ towards the right (or conversely). We clearly see then that ordinals are only a matter of order, since we constructed them by progressing along the line to the right.
In a similar way, to multiply two ordinal numbers $x$ and $y$ consists in sliding $x$ times the point $x$ to the right, and then redoing it until done $y$ times total (or conversely).
To sum up, the arithmetic of natural numbers consists in "sliding" as many times as necessary. It is a local operation in the sense we described with the analogy of the mailman : only one ordinal number is needed to have the next.
| Remark : multiplication by zero does not pose any problem. Its only particularity is that it cannot simplify because any product involving zero has the same result : zero. This is true for ordinals as well as for cardinals. |
Arithmetic of cardinal numbers
Let's use the same picture to show the profound differences with ordinal numbers. Indeed, for starters the cardinal number 0 must be represented by no point on the line, which already is a notable difference with ordinals :
 |
| Cardinal 0 |
| What does it mean ? It means that the ordinal zero and the cardinal zero have different meaning. The ordinal zero represents any empty set, whereas the cardinal zero represents... its emptiness ! |
The cardinal number 1 will be represented by one point on the line :
 |
| Cardinal 1 |
The cardinal number 2 by two points :
 |
| Cardinal 2 |
etc.
Then, to add cardinal numbers is to "melt" two lines into one :
 |
| Sum of two cardinal numbers |
To multiply two cardinal numbers $x$ and $y$ is to melt the line $x$ with $y$ copies of itself (or conversely).
Here there's no need to orient the line since the order has no importance whatsoever, and only the total "quantity" of elements on the line is of importance. It is a global operation. We cannot know the number of points on a line if we only see a part of it...
The arithmetic of cardinal numbers is better represented by sets :
 |
| Sum of two cardinal numbers |
So yeah, ordinals and cardinals are the same numbers, alright, but they definitely do not have the same role ! And it will become even clearer with infinity...
Other posts on the topic «About numbers»
Episode 1 : the natural numbers
Episode 2 : the integers
Episode 3 : rational numbers
Episode 4 : infinite numbers
Notes :
1. Cited in Eric Temple Bell, Men of Mathematics, Simon and Schuster, New York, 1986, p. 527.2. An order relation $\leq$ is a binary relation that is reflexive ($x\leq x$), transitive (if $x\leq y$ and $y\leq z$, then $x \leq z$) and antisymmetric (if $x \leq y$ and $y \leq x$ then $x = y$).
Credit :
This article and the future ones on the theme of numbers are inspired by the excellent website of Kalid Azad Better explained. See in particular his article on arithmetics. I am particularly fond of his conclusion :
« Little insights help bigger ideas click. Happy math. »
Post a Comment
You can use HTML tags b, i, a.